Контролируем моносовместимость сигнала с помощью окна Phase Analysis
Вообще-то сигнал из файла EX03_01.WAV является монофоническим и применительно к нему проблема контроля моносовместимости неактуальна. Он, безусловно, моносовместим. Такого рода контроль вам понадобится выполнять позже, когда в вашем распоряжении появятся стереофонические треки. Однако мы решили познакомить вас с возможностями окна Phase Analysis именно сейчас, в главе, посвященной всем имеющимся в программе средствам анализа оцифрованного звука.
Если вы планируете воспроизводить звуковой материал в монофоническом режиме (например, по телевидению), то должны быть уверены в его моносовместимости.
Моносовместимость важна и при передаче музыкальных композиций по радио, даже если передача ведется радиостанцией, осуществляющей стереофоническое вещание. Все дело в том, что определенная часть аудитории любой радиостанции принимает ее программы с помощью монофонических приемников. Разработчики существующих стандартов формирования стереосигналов исходили из необходимости выполнения требования совместимости стереофонической передачи с монофоническим оборудованием. Не случайно в эфир передаются не сигналы левого и правого каналов (L и R), а их сумма (L + R) и разность (L — R).
В низкочастотный тракт монофонического приемника попадает лишь суммарный сигнал, и вы можете, хоть и в монофоническом формате, но все же без каких-либо других потерь слышать все звучащие инструменты и голоса, в какой бы точке исходной стереопанорамы они ни находились.
В декодер стереофонического радиоприемника попадают и суммарный, и разностный сигналы. Там эта парочка разводится по двум каналам обработки. В одном канале сигналы, поступившие из эфира, складываются, а в другом — вычитаются. Не нужно быть профессиональным математиком для того, чтобы убедиться в справедливости элементарных преобразований:
- (L + R) + (L — R) = 2L — выделен и усилен в 2 раза сигнал левого канала (L);
- (L + R) - (L - R) = 2R — выделен и усилен в 2 раза сигнал правого канала (R).
Несовместимость музыкальной композиции с монофоническим оборудованием появляется тогда, когда компоненты звукового сигнала левого и правого каналов оказываются в противофазе. Вы уже знаете, что при преобразовании стереосигнала в монофонический сигналы левого и правого каналов суммируются. При этом звуковые компоненты, находящиеся в противофазе, "гасят" друг друга, в результате чего возникают неприятные на слух искажения. Партии некоторых инструментов могут вообще "исчезнуть" из композиции. В первую очередь это утверждение относится к партиям, панорамированным в центр.
В компьютерной музыке такая ситуация не может возникнуть сама по себе. Как правило, она является следствием применения специальных эффектов, изменяющих фазу звукового сигнала.
Определить на слух моносовместимость фонограммы способен далеко не каждый звукорежиссер. Для этой цели есть специальные устройства — контрольные дисплеи стереозвука, или стереогониометры, позволяющие анализировать множество параметров звукового сигнала, в том числе фазовые соотношения между одноименными спектральными компонентами в разных каналах.
В Adobe Audition есть возможность контроля моносовместимости сигнала с помощью встроенного в программу виртуального стереогониометра — окна Phase Analysis (рис. 4.12), открываемого командой Analize > Show Phase Analysis.
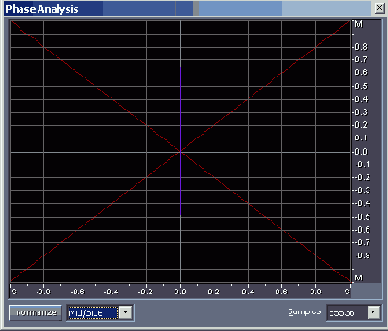
Рис. 4.12. Окно Phase Analysis; выбрана система координат M/S
Виртуальный фазовый анализатор, о котором сейчас пойдет речь, обладает функциональными возможностями, реализованными далеко не во всех его "железных" собратьях (разве что в самых дорогих). Судите сами. С помощью окна Phase Analysis можно:
- проводить анализ в реальном времени;
- получать усредненную картину для всей волновой формы;
- наблюдать мгновенную диаграмму, соответствующую текущему положению маркера;
- исследовать выделенные фрагменты волновой формы, имеющие произвольную протяженность во времени;
- отображать результаты измерений в двух различных системах координат.
Кроме координатного поля, в окне Phase Analysis еще есть только три элемента.
- Normalize — кнопка, нажав которую, вы нормализуете результаты измерения параметров сигнала таким образом, что изображение займет максимальную допустимую область координатного поля.
- Mid/Side — кнопка, предназначенная для переключения системы координат, где графически отображаются результаты измерений. Выбрать можно из трех вариантов: Mid/Side ("середина/стороны" или "моно/ стерео", см. рис. 4.12), Left/Right ("левый/правый", рис. 4.13) и Spin ("ле вый/правый с вращением развертки изображения", рис. 4.14).
- Samples — раскрывающийся список, позволяющий задать количество от счетов в анализируемом сигнале, на основе которых программа выполнит быстрое преобразование Фурье и вычислит фазовые сдвиги. Чем больше число, выбранное в этом списке, тем выше точность вычислений, но и тем больше времени они займут.
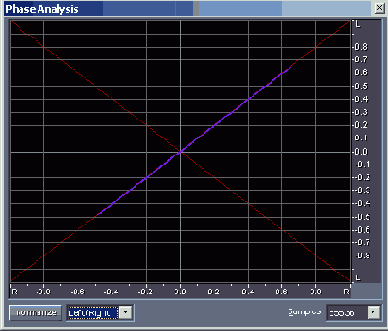
Рис. 4.13. Окно Phase Analysis. Выбрана система координат L/R
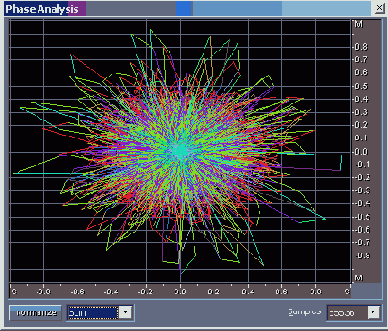
Рис. 4.14. Окно Phase Analysis. Выбран вариант отображения Spin
Окно Phase Analysis, как и рассмотренное в предыдущем разделе окно анализатора спектра, — немодальное, поэтому когда оно открыто, можно работать с элементами управления, расположенными в главном окне. В частности, можно воспроизводить записанные волновые формы и наблюдать игру красок и форм оживших графиков фазового анализатора. Кроме того, окно Phase Analysis плавающее, его можно пристыковать к границе главного окна.
Итак, с технической точки зрения применение окна Phase Analysis не составляет труда: открыли — и смотрите. Вопрос в том, что можно здесь увидеть. Прежде чем ответить на него, нужно разобраться в том, что такое фигуры Лиссажу, как они получаются и какую информацию в себе несут.
Фигурами Лиссажу называются траектории точки, одновременно совершающей гармонические колебания в двух взаимно перпендикулярных направлениях. Траектория точки — замкнутая кривая, форма которой зависит от соотношений амплитуд, частот и начальных фаз колебаний.
Текущие координаты x(t) и y(t) точки определяются системой выражений:
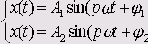
где


Фигуры Лиссажу вписываются в прямоугольник, центр которого совпадает с началом координат, а стороны параллельны осям координат (ОХ и О У) и расположены по обеим сторонам от них на расстояниях, соответственно равных А2 и А1.
Отношение частот


Во времена, когда об электронно-счетных частотомерах никто даже не мечтал, да и позже, когда они все еще оставались большой редкостью, с помощью фигур Лиссажу измеряли неизвестную частоту колебания, сравнивая ее с частой колебания эталонного.
Измерительным прибором может служить осциллограф. На пластины, отклоняющие светящуюся точку экрана в вертикальном направлении, как обычно, подают исследуемое колебание. Но, в отличие от традиционного режима работы прибора, на горизонтально-отклоняющие пластины электронно-лучевой трубки не подают сигнал, создающий временную развертку наблюдаемого процесса. Вместо него подключают эталонное гармоническое колебание. Наблюдая фигуры Лиссажу, сравнивая их с образцовыми изображениями и подсчитывая узловые точки, определяют разность фаз, отношение амплитуд и отношение частот колебаний.
Описанный принцип действия лежит в основе стереогониометра. Виртуальный аналог прибора встроен в Adobe Audition, а доступ к нему осуществляется посредством окна Phase Analysis. Работа стереогониометра поясняется схемой, представленной на рис. 4.15.
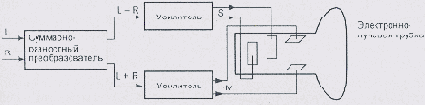
Рис. 4.15. Схема, поясняющая принцип действия стерестониометра
На два входа прибора подаются сигналы левого (L) и правого (R) каналов. Суммарно-разностным преобразователем, выполняющим функцию, обратную функции стереодекодера радиоприемника, эти сигналы преобразуются в:
- суммарный сигнал М = L + R (монофоническая компонента);
- разностный сигнал S = L — R (стереофоническая компонента).
Усиленные сигналы подаются на пластины электронно-лучевой трубки: М — на вертикально-отклоняющие, a S — на горизонтально-отклоняющие. Так складываются колебательные движения светящейся точки экрана в двух взаимно перпендикулярных направлениях — в системе координат M/S (Моно/ Стерео), т. е. образуются фигуры Лиссажу.
Точно так же действует и виртуальный стереогониометр программы Adobe Audition.
Правда, для него предусмотрен и еще один режим работы: на виртуальные отклоняющие пластины вместо суммарного и разностного сигналов подаются сигналы левого и правого каналов, а графики, соответственно, строятся в системе координат L/R (Левый/Правый).
С точки зрения информативности такие способы отображения результатов измерения равноценны. Ведь между парой сигналов L и R, с одной стороны, и их суммой и разностью, с другой стороны, есть однозначная линейная связь. Изображения одного и того же процесса, полученные в двух системах координат, оказываются очень похожими друг на друга и отличаются, в основном, направлениями своих осей. Иными словами, пользователю предлагается выбрать более привычный вариант отображения результатов измерений.
Кроме того, возможен еще вариант Spin, который имитирует вращение развертки изображения на экране. Здесь получаются картинки восхитительной красоты, но использовать их для анализа трудно. В частности, они оказываются неразличимыми в тех случаях, когда при прочих одинаковых условиях меняются местами сигналы левого и правого каналов.
Для того чтобы помочь вам освоить виртуальный стереогониометр программы Adobe Audition, приведем вид фигур Лиссажу для нескольких характерных случаев.
На рис. 4.16 представлено изображение на рабочем поле окна Phase Analysis (система координат M/S (Моно/Стерео)) для ситуации, когда сигнал присутствует только в левом канале: L

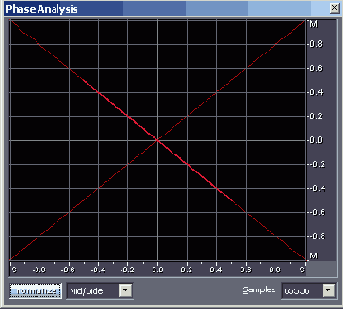
Рис. 4.16. Фигура Лиссажу: L

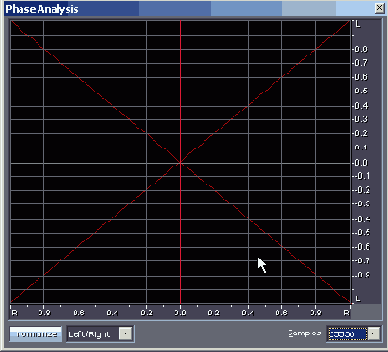
Рис. 4.17. Фигура Лиссажу: L

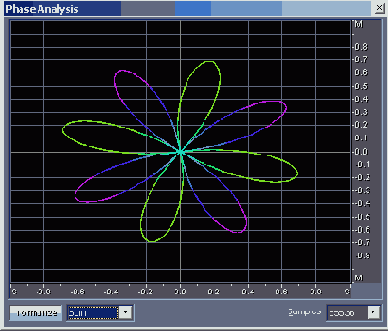
Рис. 4.18. Фигура Лиссажу: L

Заметим, что перед использованием окна Phase Analysis важно установить правильное соотношение его сторон. Очень скоро вы узнаете, что оценка моносовместимости реального сигнала производится на основе сравнения средней высоты и средней ширины изображения наблюдаемой сложной фигуры. Поэтому рабочее координатное поле должно иметь форму квадрата.
Геометрические размеры окна, как обычно, изменяют, поочередно захватывая мышью нижнюю и левую его границы. Равенство сторон координатного поля можно установить "на глазок". Этого, в принципе, достаточно. Но если вы захотите откалибровать ваш виртуальный измерительный прибор с высокой точностью, то советуем действовать в следующем порядке.
- С помощью опций окна Generate Tones, открываемого командой Generate > Tones, сгенерируйте стереофонический синусоидальный сигнал. О том, как выполняется подобная операция, рассказано в [10, разд. 7.4].
- На рабочем поле главного окна выделите волновую форму одного из каналов (например, правого) и примените команду Effects > Silence (см. [10, разд. 6.3]). После этого сигнал правого канала заменится абсолютной тишиной. Так будет смоделирована ситуация L Ф 0, R = 0.
Если вам трудно выполнить перечисленные операции, то просто загрузите в программу файл EX04_03.WAV, в котором мы записали необходимый сигнал. Откройте окно Phase Analysis. Вы увидите картину, которая должна почти в точности соответствовать рис. 4.16.
Изменяйте вертикальный и горизонтальный размеры окна в небольших пределах, наблюдая за изменениями фигуры Лиссажу (в данном случае — наклонной красной линии). Исчезновение малейших изломов на ней и послужит признаком "квадратности" координатного поля.
На рис. 4.19 в системе координат M/S представлена фигура Лиссажу для ситуации, когда сигналы присутствуют в обоих каналах, причем они равны: L = R (файл EX04_04.WAV).
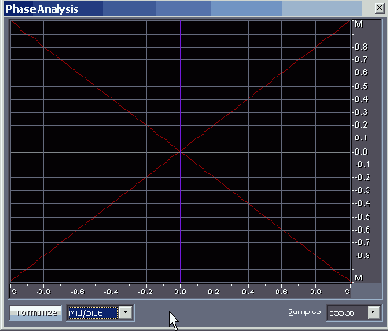
Рис. 4.19. Фигура Лиссажу: L = R, система координат M/S
На рис. 4.20 представлена фигура Лиссажу для ситуации, когда сигналы присутствуют в обоих каналах, но один из них инвертирован по отношению к другому, например, L = —R (файл EX04_05.WAV).
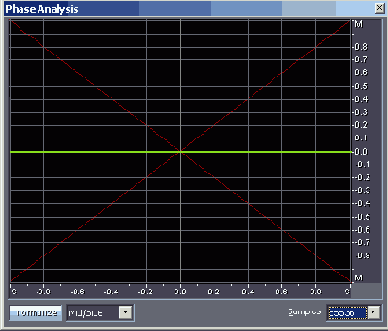
Рис. 4.20. Фигура Лиссажу: L = -R, система координат M/S
На рис. 4.21 представлена фигура Лиссажу для ситуации, когда сигналы присутствуют в обоих каналах, но наблюдается разбалансировка уровней, панорама смещена влево: L > R (файл EX04_06.WAV).
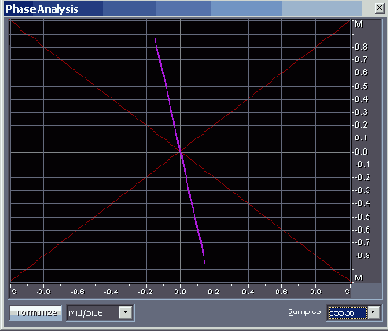
Рис. 4.21. Фигура Лиссажу: L > R, система координат M/S
На рис. 4.22 представлена фигура Лиссажу для ситуации, когда амплитуды сигналов равны (|L| = |R|), но имеется разбалансировка фаз, ф = 30° (файл EX04_07.WAV).
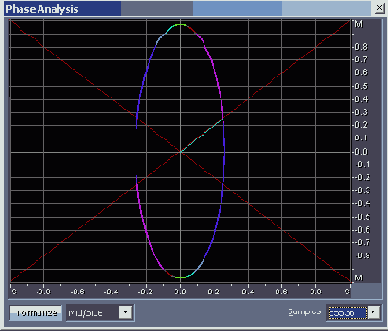
Рис. 4.22. Фигура Лиссажу:|L| = |R|, ф = 30°, система координат M/S
На рис. 4.23 представлена фигура Лиссажу для ситуации, когда амплитуды сигналов различны (|L|

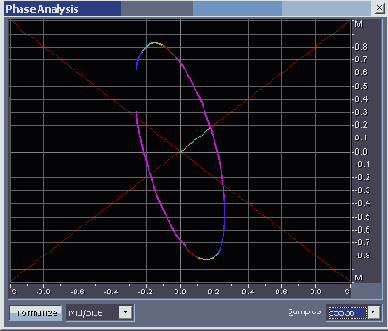
Рис. 4.23. Фигура Лиссажу: |L|

На рис. 4.24 представлена фигура Лиссажу для ситуации, когда амплитуды сигналов равны (|L| = |R|), но имеется разбалансировка фаз, ф = 90° (файл EX04_09.WAV).
Надеемся, что рассмотренные тестовые примеры помогли вам разобраться в сущности отображения сигналов в виде фигур Лиссажу. Конечно, при анализе реальных фонограмм картина на координатном поле окна Phase Analysis выглядит значительно сложнее. Ведь в ее формировании участвует не одна пара колебаний, а их теоретически бесконечное множество. Во всяком случае, спектр реального аудиосигнала чрезвычайно широк. И каждое колебание, имеющееся в спектре, характеризуется собственными параметрами: амплитудой, частотой и начальной фазой. Причем все три параметра непрерывно изменяются случайным образом.
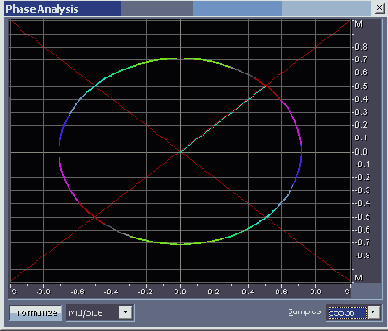
Рис, 4.24. Фигура Лиссажу: |L| = |R|, Ф = 90°, система координат M/S
И все же опытные звукорежиссеры широко используют стереогониометр и его виртуальные аналоги для определения правильности передачи звуковой картины, распределения направлений на источники звука, наличия или отсутствия баланса, фазовых соотношений и моносовместимости фонограммы.
При широкой стереобазе фонограмма является моносовместимой, если все координатное поле окна Phase Analysis заполнено сложным многоцветным рисунком с приблизительно одинаковыми размерами по различным направлениям (рис. 4.25, файл EX04_10.WAV).
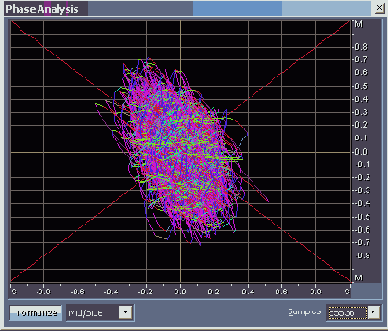
Рис. 4.25. Моносовместимая фонограмма с широкой стереобазой
У фонограммы, характеризующейся узкой стереобазой, признак моносовместимости заключается в том, что фигуры на координатном поле в основном вытянуты вдоль вертикальной оси (рис. 4.26, файл EX04_ll.WAV).
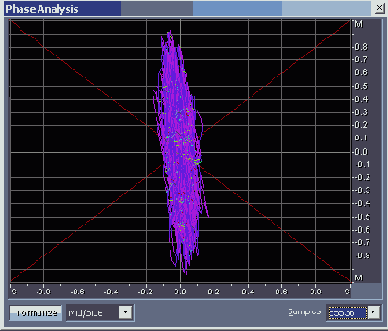
Рис. 4.26. Моносовместимая фонограмма с узкой стереобазой
Фонограмма мононесовместима, когда фигуры на координатном поле растянуты вдоль горизонтального направления (рис. 4.27, файл EX04_12.WAV).
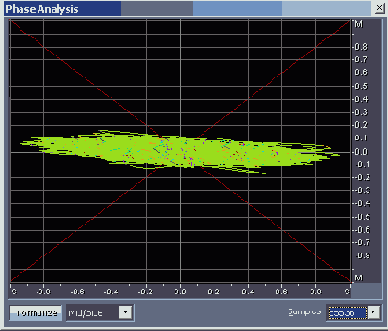
Рис. 4.27. Мононесовместимая фонограмма
Если большая ось изображения на координатном поле отклонена от вертикали, то это является признаком нарушения стереобаланса: панорама сдвинута вправо (рис. 4.28, файл EX04_13.WAV) или влево (рис. 4.29, файл EX04_14.WAV).
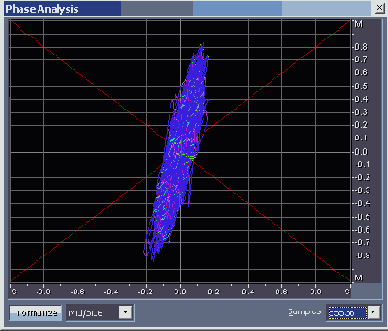
Рис. 4.28. Панорама сдвинута вправо
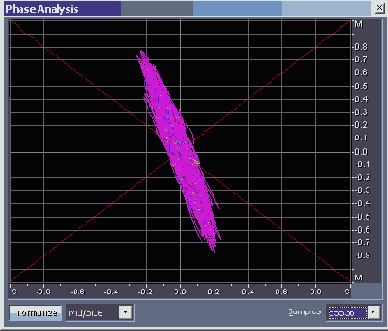
Рис. 4.29. Панорама сдвинута влево
Проанализируйте свои работы с помощью окна Phase Analysis. Скорее всего, вы обнаружите много поучительного и увидите ошибки, о которых раньше и не подозревали.